 |
AutoFEM Analysis Vibrations of a Spring-Mass System Because of Oscillating Foundation | ||||||
Vibrations of a Spring-Mass System Because of Oscillating Foundation
Let us consider the mass- spring system. The spring is attached to vibrating base, vibrations of which are harmonic. The amplitude of oscillation is equal to 1.34192762 mm.
|
Let us use the following initial data: the mean diameter of the spring D is 30 mm, the length of the spring H is 100 mm, the cross section of the wire is a square with a side d=3 mm, the number of spring turns n is 6. Parameters of a weight are following: the diameter DW= 40 mm, height H=35 mm, mass mW= 0.34306 kg.
Parameters of the spring/weight material: modulus of elasticity E=2.1E+011Pa, Poisson's ratio ν=0.28, density ρ=7800kg/m3, shear modulus G=8.203E+010Pa, damping coefficient 2 % relatively the critical damping.
Our aim is to find oscillation amplitudes of the mass, using the frequencies, which ranges from 5Hz to 30Hz. The ratios of the Rayleigh damping have following values: α= 0.02, β= 2.6891E-004. These values correspond to 2% of the critical resistance.
Amplitude of forced harmonic oscillations for the system with one degree of freedom is described according to the following formula:

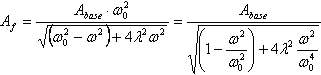 , (1)
, (1)
where Abase  is an amplitude of oscillation of the base,ω is the angular frequency of the oscillations of the base, ω0 is the natural angular frequency of the oscillations of the system, λ is the damping coefficient.
is an amplitude of oscillation of the base,ω is the angular frequency of the oscillations of the base, ω0 is the natural angular frequency of the oscillations of the system, λ is the damping coefficient.
Let us denote the expression λ/ω0= γ, then the formula (1) goes over:
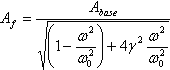 , (2)
, (2)
where the coefficient γ will be calculated by the following formula:
![]() . (3)
. (3)
The coefficients α, β are the mass damping coefficient and the stiffness damping coefficient, respectively.
The spring stiffness is calculated by the formula:
![]() . (4)
. (4)
Thus, the spring has following stiffness:
![]() .
.
Then the natural angular frequency is
![]() ,
,
and the natural frequency is
![]() .
.
Let us calculate the amplitudes A f by the formula (2) for the frequencies f1=5Hz, f2=10Hz, f3=15Hz, f4=20Hz, f5=f0, f6=25Hz, f7=30Hz and γ=0.02.
Thus, A1f= 1.4057 mm, A2f= 1.6396 mm, A3f= 2.2682 mm, A4f=4.8773 mm, A5f= 33.8482 mm, A6f= 9.4208 mm, A7f= 2.1041 mm.
Let us solve this study by AutoFEM Analysis.
The top end of the spring is oscillating with amplitude being equal to 1.34192762 mm. Displacements of the weight along X-axis and Y-axis are forbidden.
|
The finite element model with applied loads and restraints |
After carrying out calculations by the AutoFEM Analysis the following results are obtained:
Table 1. Parameters of the finite element mesh
Finite element type |
Number of nodes |
Number of finite elements |
quadratic tetrahedron |
2675 |
6613 |
Table 2.The result “Amplitude”
Frequency, Hz |
Numerical solution |
Analytical solution |
Error |
5 |
1.406 |
1.4057 |
0.02 |
10 |
1.640 |
1.6396 |
0.02 |
15 |
2.262 |
2.2682 |
0.27 |
20 |
4.755 |
4.8773 |
2.51 |
f0=23.634 |
34.150 |
33.8482 |
0.89 |
25 |
10.890 |
9.4208 |
15.6 |
30 |
2.260 |
2.1041 |
7.41 |
|
*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.
Read more about AutoFEM Oscillations Analysis